Es ist einfacher zu erklären. soziale A/B-Tests unter Verwendung dieser Analogie:
Tu so, als hättest du noch nie einen Hund gesehen. (Arbeite mit mir hier.) Du stehst auf deinem Lieblingsgehweg und siehst einen vorbeigehen. Und es ist rosa. Da Sie keine Vorkenntnisse darüber haben, wie Hunde aussehen sollen, glauben Sie wahrscheinlich jetzt, dass alle Hunde rosa sind. Wie seltsam.
Dann siehst du einen zweiten Hund vorbeigehen. Es ist schwarz. Mit diesem neuen Wissen sind Sie nun der Meinung, dass 50% der Hunde rosa und 50% schwarz sind. Du hast an dieser Stelle keine Möglichkeit zu wissen, dass ein rosa Hund ein Ausreißer ist, etwas, das du vielleicht nie wieder sehen wirst.
Lasst es uns wieder in die Realität umsetzen. Du weißt, wie Hunde aussehen. Wenn Sie einen rosa Hund sehen, erkennen Sie ihn sofort als ungewöhnlich, ja, unmöglich ohne Farbstoff. Sie können nun jedoch zulassen, dass ein kleiner Prozentsatz der Hunde rosa ist. Herzlichen Glückwunsch, du hast das Bayes'sche Denken auf die Farbe der Hunde angewendet!
Was hat das mit A/B-Tests zu tun? So offensichtlich es auch für uns ist, Ausreißer in der Farbe des Hundes zu erkennen, so viel schwieriger ist es, dieses Denken anzuwenden, wenn es um Bekehrungen, Klicks oder Engagement geht. Nehmen wir ein Beispiel.
Anstatt auf dem Bürgersteig zu stehen und frische Luft zu genießen, sitzen Sie jetzt an Ihrem Schreibtisch und beobachten die Ergebnisse Ihres letzten A/B-Tests. Sie sehen, dass die Variante 1 Ihres Tests eine respektable Klickrate von 5% aufweist. Die Variante 2 sieht mit 26% noch besser aus. Sie klopfen sich selbst auf die Schulter, weil Sie das gefunden haben, Überschriftdas 400% besser engagiert!
"Aber warte", höre ich dich sagen. "Eine 26%ige Klickrate? Das sieht wirklich aus wie ein rosa Hund." Und in der Tat ist es das wahrscheinlich auch. Sie haben jetzt das Bayes'sche Denken auf A/B-Tests angewendet, und damit haben Sie sich selbst davon abgehalten, diese @channel Slack-Nachricht zu senden, die Ihre A/B-Testfähigkeiten verkündet. Stattdessen wenden Sie zunächst eine gründliche Analyse Ihrer Ergebnisse an.
Hier ist, wie man es macht.
Unser Ziel
Lassen Sie uns das etwas konkreter machen. Wir verwenden ein Beispiel aus der Praxis mit freundlicher Genehmigung eines unserer Verlagspartner. Soziales A/B-Tool um A/B-Tests durchzuführen. Dieser spezielle Kunde möchte die Einführungskopie eines Facebook-Posts testen. Hier sind die Varianten:
Variante 1:
"Folge Mikey Rencz, Mikkel Bang und Mark Sollors in Episode drei von Burton Presents. Schau unten."
Variante 2:
"Das Leben eines Burton-Profis."
Wir wollen erfahren, welche dieser beiden Beiträge auf Facebook am besten funktionieren und um wie viel. Zu diesem Zweck werden wir jede Variation an eine kleine repräsentative Stichprobe des HerausgeberPublikums senden und die Leistung jeder Variation im Laufe der Zeit verfolgen. Glücklicherweise, Soziale A/B automatisiert diesen Prozess für Sie. Nach einiger Zeit (normalerweise einige Minuten) werden wir Daten von Facebook erhalten. Dann beginnt der wahre Spaß.
Der naive Ansatz der A/B-Testergebnisanalyse
Der einfachste Weg, die Leistung eines Beitrags zu berechnen, ist der folgende:
- Holen Sie sich die Klicks und greifen Sie für jede Variante.
- Teilen Sie Klicks nach Reichweite, um die Click-Through-Rate (CTR) zu erhalten.
- Berechnen Sie, wie viel besser das eine besser ist als das andere.
Erfahrenere Tester werden einen Stichprobengrößenrechner verwenden, um zu bestätigen, dass die Stichprobe groß genug ist, um signifikant zu sein. Dies ist ein entscheidender Schritt. Aber wir glauben nicht, dass es genug ist. Hier ist der Grund....
Nehmen wir an, nachdem wir die beiden Varianten 20 Minuten lang einem repräsentativen Sample-Publikum ausgesetzt haben, erhalten wir diese Ergebnisse:
- Variante 1: 46 Klicks, 866 Impressionen = 5,3% CTR
- Variante 2: 8 Klicks, 676 Impressionen = 1,2% CTR
Die Variation 1 übertraf die Variation 2 in diesem Beispiel um 340%. Legitim? Ein schneller Chi-Quadrat-Test bestätigt, dass wir genügend Daten haben, um eine Schlussfolgerung zu ziehen, und so sind wir zuversichtlich.
Aber jetzt geben wir ihm den Pink Dog Test. Wann hatten Sie das letzte Mal ein Post-Drive über 5% Klickrate? Niemals? Okay, ist dieser Beitrag, der Nachrichten verbreitet, oder über das weiß-goldene Kleid? Nein? Es ist eine Geschichte über rosa Hunde? Vielleicht ist die Klickrate einen weiteren Blick wert.
Dieser Ansatz ignoriert die Realität dessen, was normalerweise auf deinen Beiträgen passiert, und öffnet die Tür für wild ungenaue Annahmen. Es kann immer noch die bessere Variation genau vorhersagen, aber wie viel besser? Wenn Variante 1 46 Klicks auf 866 Impressionen erhielt, wird sie dann wirklich 460 auf 8.660 Impressionen erhalten? Es ist möglich, aber wenn man eine wichtige redaktionelle Entscheidung trifft und A/B-Testsiege erzielt, ist es besser, auf der Seite des vorsichtigen Optimismus zu lüften als auf der Seite der hoffnungsvollen Ausgelassenheit. Verwenden wir also die gleichen Daten, aber berücksichtigen wir unsere Vorkenntnisse.
Der Bayes'sche Ansatz
Als Sie den rosa Hund als Anomalie erkannten, taten Sie dies aufgrund Ihrer Vorkenntnisse (oder Ihres Glaubens) über die natürliche Farbe der Hunde. Du hast auch diesen neuen Datenpunkt (einen einzelnen rosa Hund) zu deinem Wissen hinzugefügt, was ihn zum neuen vorherigen Glauben für dein zukünftiges Selbst macht. Das ist das Grundprinzip des Bayes'schen Denkens. Und das ist es, was wir bei der Analyse von Testergebnissen tun müssen. Warum? Weil Sie eine Menge Wissen darüber haben, wie sich Ihre Inhalte und Ihr Publikum in der Regel verhalten. Es gibt keinen Grund, dieses Wissen zu ignorieren, wenn man die zukünftige Leistung voraussagt.
Die erste Herausforderung, vor der wir stehen, besteht darin, unseren bisherigen Glauben an die Leistung von Facebook-Posts zu quantifizieren. Dieser mathematische Vorglaube muss zwei Dinge darstellen:
- Ihre übliche Click-Through-Rate
- Die typische Abweichung der Klickraten zwischen den Beiträgen
HerausgeberIn unserem Beispiel sehen die meisten Facebook-Posts eine Klickrate zwischen 1% und 2%, ohne große Abweichungen. Wir könnten dies als Mittelwert und als Standardabweichung darstellen, aber nützlicher für die Berechnungen, die wir durchführen müssen, ist es, das Wissen als so genannte Alpha- (α) und Beta-Parameter (β) darzustellen. Beginn: Magie.
Die α und β dafür Herausgebersind 12,92 und 842,22. Wir werden diskutieren, wie diese an einem Regentag berechnet werden. Für den Moment sollten Sie nur wissen, dass sie die erwartete Klickrate eines Beitrags darstellen und dass ihre Größe umgekehrt mit der Varianz der Klickraten korreliert.
Um unsere Arbeit noch einmal zu überprüfen, nutzen wir unsere Website α und β, um unsere erwartete Klickrate zu berechnen. Das können wir mit einer einfachen Formel erreichen:
Erwartete CTR = α / (α + β) = 12,92 / (12,92 + 842,22) = 1,5%.
Dies entspricht unserer früheren Überzeugung über die Leistung nach dem BeitrittHerausgeber. Wie können wir dies nutzen, um zukünftige Klickraten auf unsere Beiträge vorherzusagen? Es ist Magie, weil es so einfach ist:
Voraussichtliche CTR = (Klicks + α) / (erreichen Sie + α + β)
Was? Mathe der 8. Klasse? Ich muss es lieben. Lassen Sie uns dies also nutzen, um unsere vorhergesagte Klickrate zu berechnen, da die Daten aus unserem realen Test, den wir oben erwähnt haben, stammen:
| Minute | Variante 1 Klicks/Reichweite - CTR | Variante 2 Klicks/Reichweite - CTR | Variante 1 Vorhergesagte CTR | Variante 2 Vorhergesagte CTR |
|---|
| 0 | 0/0 – 0% | 0/0 – 0% | 1.5% | 1.5% |
| 5 | 2/200 – 1% | 4/174 – 2.3% | 1.41% | 1.64% |
| 10 | 12/260 – 4.6% | 4/290 – 1.4% | 2.23% | 1.48% |
| 15 | 36/698 – 5.2% | 6/578 – 1% | 3.15% | 1.32% |
| 20 | 46/866 – 5.3% | 8/676 – 1.2% | 3.42% | 1.37% |
In Minute 0, bevor wir unseren Beitrag getestet haben, gibt uns die Formel eine vorhergesagte Klickrate, die unserem vorherigen Glauben entspricht. Macht Sinn, denn wenn wir keine neuen Informationen haben, ist unser wahrscheinlichstes Ergebnis gleich unserem vorherigen Glauben.
Schauen Sie sich nun Minute 20 an, wo wir eine Klickrate von 5,3% für die Variante 1 beobachteten. Es ist verlockend, zu verkünden, wie gut diese Variation ist, aber wenn wir unser Vorwissen berücksichtigen - sowohl die durchschnittliche Klickrate dafür als Herausgeberauch die erwartete Varianz, wie sie in unseren Parametern α und β dargestellt ist - sehen wir, dass es viel wahrscheinlicher ist, dass die tatsächliche Klickrate 3,4% beträgt.
Um die Intuition in diesem Beispiel abzurunden, lassen Sie uns so tun, als hätten wir eine viel größere Population, und diese Klickrate der Variante 1 beträgt tatsächlich 5,3%. Um zu sehen, wie diese Formel funktioniert, multiplizieren wir die 20-Minuten-Ergebnisse der Variante 1 mit 1.000.
Voraussichtliche CTR = (46000 + 12,92) / (866.000 + 19,92 + 842,22)
Voraussichtliche CTR = 5,3%.
Du wirst zwei Dinge bemerken:
- Wenn wir mehr Daten erhalten, werden wir zuversichtlicher, dass die beobachtete Klickrate tatsächlich unsere vorhergesagte Klickrate ist.
- Je größer die Parameter α und β, desto mehr Daten benötigen wir, um unsere Vorhersage zu verschieben.
Herzlichen Glückwunsch, Sie haben den Bayes'schen Teil der Analyse abgeschlossen! Lassen Sie uns nun unsere Prognosen nutzen, um einen Gewinner auszuwählen.
Messgenauigkeit
Bevor wir über Präzision sprechen, müssen wir über Wahrscheinlichkeitsdichtefunktionen sprechen. Beherrschen Sie sich, der aufregendste Teil kommt noch!
Die Parameter α und β bilden die Grundlage für die Wahrscheinlichkeitsdichtefunktion (PDF) einer Beta-Verteilung. Im Englischen sagt uns dies die Wahrscheinlichkeit, dass unsere Klickrate ein bestimmter Wert ist. Beispiel:
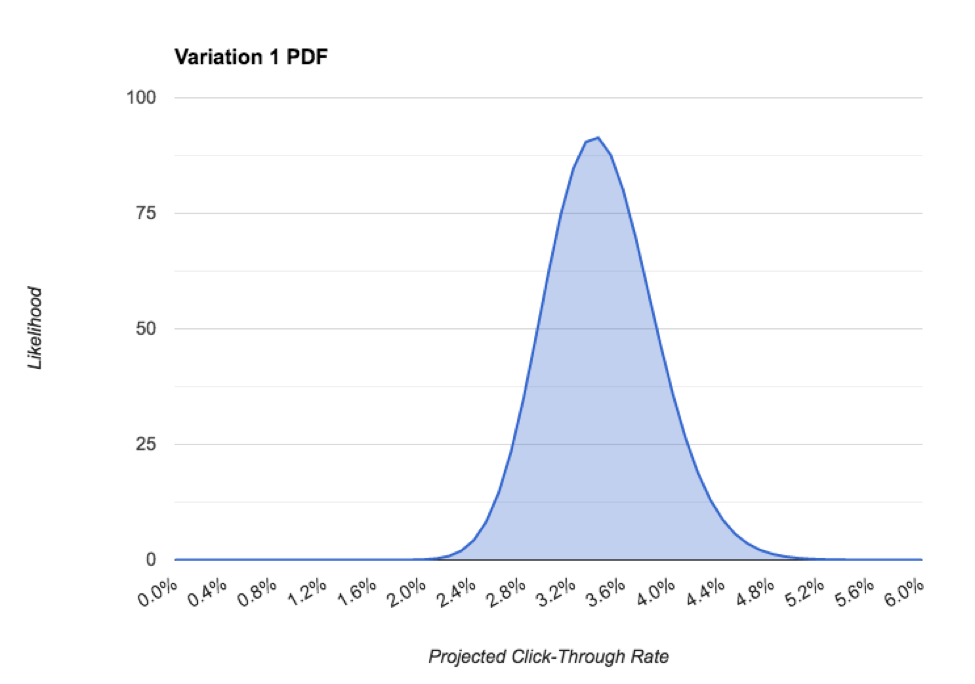
In dem obigen PDF sehen wir die wahrscheinlichste Klickrate für diesen Beitrag ist etwa 3,4%. Messung ist das glaubwürdige Intervallwas der 95%igen Verteilung des PDF entspricht, was in unserem Fall etwa 2,2% entspricht. Wenn wir mehr Daten sammeln und mehr Vertrauen in unsere Vorhersage haben, verbessert sich die Präzision, was für die Auswahl eines Gewinners entscheidend ist. Das werden wir als nächstes angehen.
Berechnung der Wahrscheinlichkeit
Wir sind endlich angekommen. Es ist an der Zeit, herauszufinden, ob unsere bessere Variante tatsächlich ein Gewinner ist! Beginnen wir damit, es zu visualisieren.
Hier ist das PDF der beiden Varianten, auf einem Diagramm:
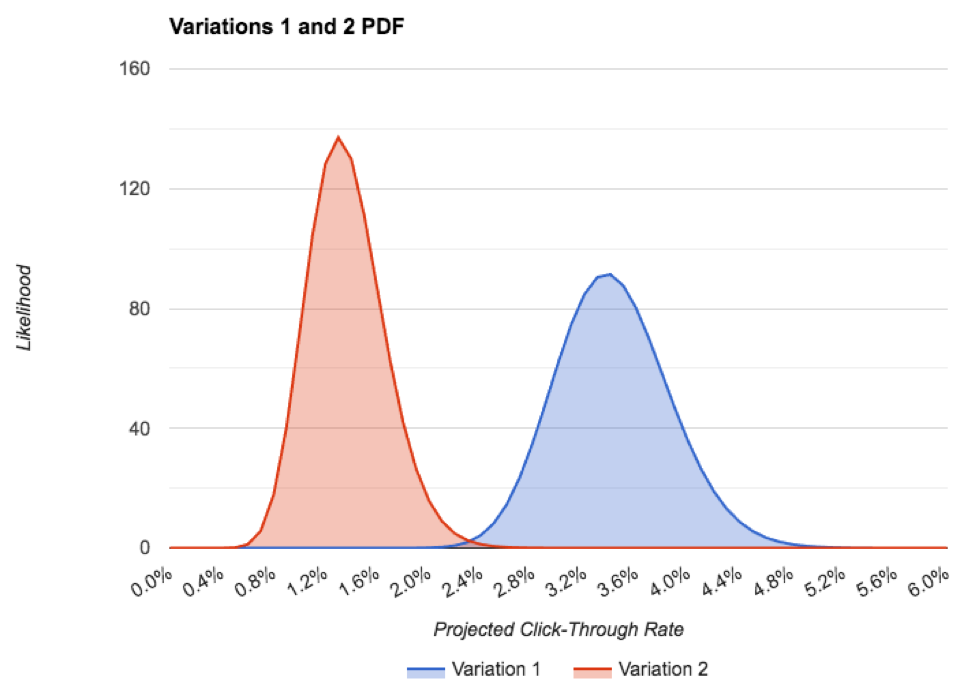
Sie können sehen, dass die Genauigkeit der Variante 1 geringer ist als die der Variante 2, obwohl wir etwas mehr Daten haben. Das liegt daran, dass es ziemlich weit von der erwarteten, vorherigen Klickrate entfernt ist. Dennoch gibt es kaum Überschneidungen zwischen den PDFs, was für unseren Test sehr gut ist!
Die einzige Möglichkeit, wie Variation 2 tatsächlich besser ist als Variation 1, ist, wenn die tatsächliche zukünftige Klickrate der Variation 2 mehr als 2% betrug und die tatsächliche zukünftige Klickrate der Variation 1 weniger als etwa 2,2% betrug, was jeweils sehr unwahrscheinlich ist. Dies wird durch die geringe Überlappung der beiden PDFs dargestellt. Damit beide Anomalien auftreten, wäre es, als würden Dutzende von Köpfen in Folge auf eine faire Münze geworfen. Das wird nicht passieren.
Daher sind wir an dieser Stelle sehr zuversichtlich, dass Variante 1 der Gewinner ist und dass sie etwa 3,4% CTR gegenüber Variante 2 mit 1,4% fahren sollte.
Jetzt können wir es sehen, berechnen wir es.
Der lustige (langsame) Weg
Die lustige Art, die Wahrscheinlichkeit zu messen, dass eine Variation wirklich besser ist als die andere, ist die Ausführung einer Markov Chain Monte Carlo-Simulation. Für unsere Testergebnisse erhalten wir nach 1.000.000.000 Iterationen eine Wahrscheinlichkeit von 0,999, dass Variation 1 die beste ist. Großartig!
Der Nachteil ist, dass ein MCMC tatsächlich Software benötigt, um etwas Millionen Mal zu tun. Wer hat so viel Zeit?
Der langweilige (schnelle) Weg
Zum Glück für uns gibt es einige kluge Leute, die clevere Formeln entwickelt haben. damit wir es nicht selbst simulieren müssen.
Nachdem wir unsere Zahlen eingesteckt haben und ein paar Millisekunden gewartet haben, sehen wir, dass Variation 1 besser ist als 2 mit einer Wahrscheinlichkeit von 1,0. Der Sieg gehört uns!
Lassen Sie uns alle Schritte zusammenfassen, die wir unternommen haben, um unseren Test erfolgreich abzuschließen:
- Wir haben uns vorher auf die erwartete Klickrate unserer Beiträge festgelegt, die durch die Parameter α und β repräsentiert wird.
- Wir zeigten jede Variation einer repräsentativen Stichprobe unseres Publikums und sammelten dabei Klick- und Reichweitendaten von Facebook.
- Wir haben unsere vorherige Überzeugung und die Daten, die wir aus unserem Test gezogen haben, genutzt, um die wahrscheinliche Klickrate für jeden Beitrag zu berechnen.
- Wir haben uns das PDF unserer Seitenzähne angesehen, um sicherzustellen, dass wir über genügend Daten verfügen, die durch die erforderliche Präzision informiert sind.
- Wir verwendeten eine ausgefallene Formel, um die Wahrscheinlichkeit zu berechnen, dass unsere leistungsstärkere Variante tatsächlich die beste ist.
Jetzt ist es an der Zeit, die Ergebnisse Ihres A/B-Tests in @channel #general zu veröffentlichen, da Sie wissen, dass Ihr Gewinner echt ist und dass er mehr soziales Engagement fördert und zu Ihren erstaunlichen Inhalten zurückkehrt. Was hoffentlich mit rosa Hunden zu tun hat.
Weiterführende Literatur
Die Konzepte in diesem Blogbeitrag und die von unserem Tool verwendeten Methoden profitierten stark von der durchdachten Arbeit mehrerer Datenwissenschaftler und Statistiker. Wir empfehlen dringend, tiefer in diese Konzepte einzutauchen, indem wir ihre Arbeit lesen:
- Wie A/B-Tests funktionieren
- Ignorant No More: Crashkurs zur A/B-Teststatistik
- Statistische Signifikanz ist nicht gleichbedeutend mit der Gültigkeit.
- Wie man einen A/B-Test nicht durchführt
- A/B-Test mit hierarchischen Modellen in Python
- Bayes'sche Banditen
- Statistische Hinweise zur A/B-Prüfung
- Formeln für die Bayes'sche A/B-Prüfung
- Verständnis der empirischen Bayes'schen hierarchischen Modellierung
- Die gesamte Serie "Using Baseball Statistics" ist hervorragend.
Möchten Sie mehr erfahren?
A/B Das Testen Ihrer Inhalte auf Facebook ist ein komplexes Thema. Wir haben für Sie alles im Griff - Sie können mehr darüber erfahren:
- Optimierung von Inhalten für den Änderungsalgorithmus von Facebook
- Erstellung einer effektiven Intro-Kopie
- Designen von klickwürdigen Facebook-Anzeigen
Setzen Sie sich auf den Fahrersitz und starten Sie A/B, um Ihre Inhalte für Facebook zu testen. Es dauert weniger als eine Minute, bis Sie sich für unsere Soziales A/B-Tool und es ist völlig kostenlos - also warum nicht eine Spritztour machen?