Es más fácil de explicar Pruebas A/B para redes sociales Pruebas usando esta analogía:
Finge que nunca has visto un perro. (Trabaja conmigo aquí.) Estás parado en tu acera favorita y ves pasar uno. Y es rosa. Basándose en no tener conocimiento previo de lo que los perros se supone que parecen, es probable que ahora cree que todos los perros son de color rosa. Qué raro.
Entonces ves a un segundo perro pasar. Es negro. Con este nuevo conocimiento, ahora consideras que el 50% de los perros son de color rosa y el 50% son negros. Usted no tiene manera de saber en este punto que un perro rosado es un afloramiento, algo que usted puede ser que nunca vuelva a ver.
Vamos a traerlo de vuelta a la realidad. Ya sabes como son los perros. Cuando ves a un perro rosado, inmediatamente lo reconoces como inusual, de hecho, imposible sin tinte. Sin embargo, ahora puede permitir que algunos pequeños porcentajes de perros son de color rosa. ¡ Felicitaciones, has aplicado el pensamiento Bayesiano al color de los perros!
¿Qué tiene que ver esto con las pruebas A/B? Por obvio que es para nosotros reconocer los valores atípicos en el color de los perros, es mucho más difícil aplicar este pensamiento cuando se miran conversiones, clics o compromiso. Vamos a tomar un ejemplo.
En lugar de estar en la acera disfrutando de aire fresco, ahora está sentado en su escritorio, observando los resultados de su última prueba A/B. Usted ve que la variación 1 de su prueba tiene una tasa respetable del 5% de clic-through. La variación 2 se ve aún mejor al 26%. ¡ Usted se acaricia en la parte posteriora para encontrar el título que enganchará a 400% mejor!
"Pero espera", te oigo decir. "Un 26% de clic-a través de la tarifa? Que se parece mucho a un perro de color rosa. Y, de hecho, probablemente lo es. Ahora has aplicado el pensamiento Bayesiano a la prueba de A/B, y al hacerlo, te has detenido a ti mismo de enviar ese @channel mensaje flojo proclamando tu destreza de prueba de A/B. En su lugar, primero aplicará un análisis riguroso a sus resultados.
Así es como hacerlo.
Nuestro objetivo
Hagamos esto un poco más concreto. Usaremos un ejemplo del mundo real por cortesía de uno de nuestros socios editoriales Pruebas A/B para redes sociales Herramienta para ejecutar pruebas A/B. Este cliente en particular quiere probar la copia de introducción de un puesto de Facebook. Aquí están las variaciones:
Variación 1:
"Sigue a Mikey Rencz, Mikkel Bang, y Mark Sollors alrededor en el episodio tres de Burton Presents. Ver abajo.
Variación 2:
"La vida de un Burton Pro".
Queremos saber cuál de estos dos puestos se realizará mejor en Facebook, y por cuánto. Para ello, publicaremos cada variación en una pequeña muestra representativa de la audiencia del editor y rastrearemos el rendimiento de cada variación con el tiempo. Afortunadamente Social A/B automatiza este proceso para usted. Después de algún tiempo (usualmente unos minutos), recibiremos datos de Facebook. Ahí es cuando comienza la verdadera diversión.
El acercamiento ingenuo al análisis del resultado de la prueba de A/B
La forma más fácil de calcular el rendimiento de un post es la siguiente:
- Obtener los clics y llegar a cada variación
- Divida los clics por Reach para obtener la tasa de clic (CTR)
- Calcular cuánto mejor uno es que el otro
Los probadores más sofisticados usarán una calculadora de tamaño de muestra para validar que la muestra es lo suficientemente grande como para ser significativa. Este es un paso crítico. Pero no creemos que sea suficiente. He aquí por qué...
Digamos que después de exponer las dos variaciones a una audiencia de muestra representativa durante 20 minutos, recibimos estos resultados:
- Variación 1:46 clics, 866 impresiones = 5,3% CTR
- Variación 2:8 clics, 676 impresiones = 1,2% CTR
Variación 1 superó la variación 2 en este ejemplo por 340%. ¿Legítimo? UNA prueba de Chi-cuadrado rápida valida que tenemos suficientes datos para formar una conclusión, y así nos sentimos confiados.
Pero ahora vamos a darle la prueba de perro rosa. ¿Cuándo fue la última vez que tuvo una unidad de correo más del 5% de velocidad de clic? ¿Nunca? Bien, ¿esto es noticia de última hora, o sobre el vestido blanco y dorado? ¿No? ¿Es una historia sobre perros rosas? Tal vez la tasa de click-through valga otra mirada.
Este enfoque ignora la realidad de lo que suele ocurrir en sus puestos, abriendo la puerta para suposiciones tremendamente inexactas. Todavía puede predecir con precisión la mejor variación, pero ¿cuánto mejor? Si la variación 1 tiene 46 clics en 866 impresiones, ¿realmente obtendrá 460 en 8.660 impresiones? Es posible, pero al formar una importante decisión editorial y reclamar las victorias A/B, es mejor ventilar el lado del optimismo prudente que la exuberancia esperanzadora. Así que usemos los mismos datos, pero tomemos en cuenta nuestro conocimiento previo.
El enfoque Bayesiano
Cuando reconoció al perro rosado como una anomalía, lo hizo debido a su conocimiento previo (o creencia) sobre el color natural de los perros. Usted también agregó este nuevo punto de datos (un solo perro rosado) a su conocimiento, haciéndole la nueva creencia anterior para su uno mismo futuro. Este es el concepto fundamental del pensamiento Bayesiano. Y es lo que tenemos que hacer al analizar los resultados de las pruebas. ¿Porqué? Porque usted tiene un montón de conocimientos acerca de cómo su contenido y el público suelen realizar. No hay razón para ignorar ese conocimiento al predecir el rendimiento futuro.
El primer desafío que enfrentamos es cuantificar nuestra creencia previa sobre el rendimiento de post de Facebook. Esta creencia matemática previa necesita representar dos cosas:
- Su tarifa usual de click-through
- La variación típica de las tasas de clic entre los mensajes
Para el editor en nuestro ejemplo, la mayoría de los mensajes de Facebook ven entre el 1% y el 2% de la tarifa de clic-through, sin mucha variación. Podríamos representar esto como una media y una desviación estándar, pero más útil para los cálculos que necesitamos hacer es representar el conocimiento como lo que se llama alfa (α) y beta (β) parámetros. Begin: Magic.
El α y el β para este editor son 12,92 y 842,22, respectivamente. Discutiremos cómo se calculan en un día lluvioso. Por ahora, sólo sepan que representan la tasa de click-through prevista de un post, y que su magnitud está inversamente correlacionada con la variación de los índices de clics.
Para comprobar el doble de nuestro trabajo, usemos nuestro α y β para calcular nuestra tarifa esperada de click-through. Podemos hacerlo con una fórmula sencilla:
CTR esperado = α/(α + β) = 12,92/(12,92 + 842,22) = 1,5%
Esto coincide con nuestra creencia previa sobre el rendimiento post del editor. ¿Cómo usamos esto para predecir las futuras tarifas de click-through en nuestros posts? Es mágico porque es simple y muerto:
CTR preDicho = (clics + α)/(alcance + α + β)
¿Qué? ¿matemáticas de octavo grado? Tengo que amarlo. Así que vamos a utilizar esto para calcular nuestra tasa de clic-through predicho como los datos llegaron de nuestra prueba del mundo real que hemos tocado arriba:
| Minuto | Variación 1 Clicks/Reach - CTR | Variación 2 Clicks/Reach - CTR | Variación 1 CTR preDicho | Variación 2 CTR preDicho |
|---|
| 0 | 0/0 – 0% | 0/0 – 0% | 1.5% | 1.5% |
| 5 | 2/200 – 1% | 4/174 – 2.3% | 1.41% | 1.64% |
| 10 | 12/260 – 4.6% | 4/290 – 1.4% | 2.23% | 1.48% |
| 15 | 36/698 – 5.2% | 6/578 – 1% | 3.15% | 1.32% |
| 20 | 46/866 – 5.3% | 8/676 – 1.2% | 3.42% | 1.37% |
En el minuto 0, antes de que hayamos probado nuestro post, la fórmula nos da una tasa de click-through predicha que es igual a nuestra creencia previa. Tiene sentido, ya que si no tenemos ninguna información nueva, nuestro resultado más probable es igual a nuestra creencia previa.
Ahora eche un vistazo al minuto 20, donde observamos un 5,3% de clic-a través de la tasa de variación 1. Es tentador proclamar lo buena que es esta variación, pero cuando tomamos en cuenta nuestro conocimiento previo, tanto la tasa promedio de click-through para este editor como la varianza esperada representada en nuestros parámetros α y β, vemos que es mucho más probable que el la tasa real de clic es 3,4%.
Para redondear la intuición en este ejemplo, finjamos que tenemos una población mucho más grande, y que la tasa de clic-through de variación 1 es en realidad 5,3%. Para ver cómo funciona esta fórmula, multiplicaremos los resultados de 20 minutos de variación 1 por 1.000.
CTR preDicho = (46000 + 12,92)/(866.000 + 19,92 + 842,22)
CTR preDicho = 5,3%
Puede notar dos cosas:
- A medida que conseguimos más datos, nos volvemos más seguros de que la tasa de clic-through observado en realidad es nuestra tasa de click-through predicha
- Cuanto más grandes sean los parámetros α y β, más datos necesitamos para mover nuestra predicción
¡ Enhorabuena, has completado la parte Bayesiano del análisis! Ahora vamos a usar nuestras predicciones para elegir un ganador.
Precisión de medición
Antes de hablar de precisión, tenemos que hablar de las funciones de densidad de probabilidad. ¡ ConTengase, la parte más emocionante está todavía por venir!
Los parámetros del α y del β forman la base para la función de la densidad de la probabilidad (PDF) de una distribución beta. En inglés, esto nos dice la probabilidad de que nuestra tasa de click-through sea un cierto valor. Ejemplo:
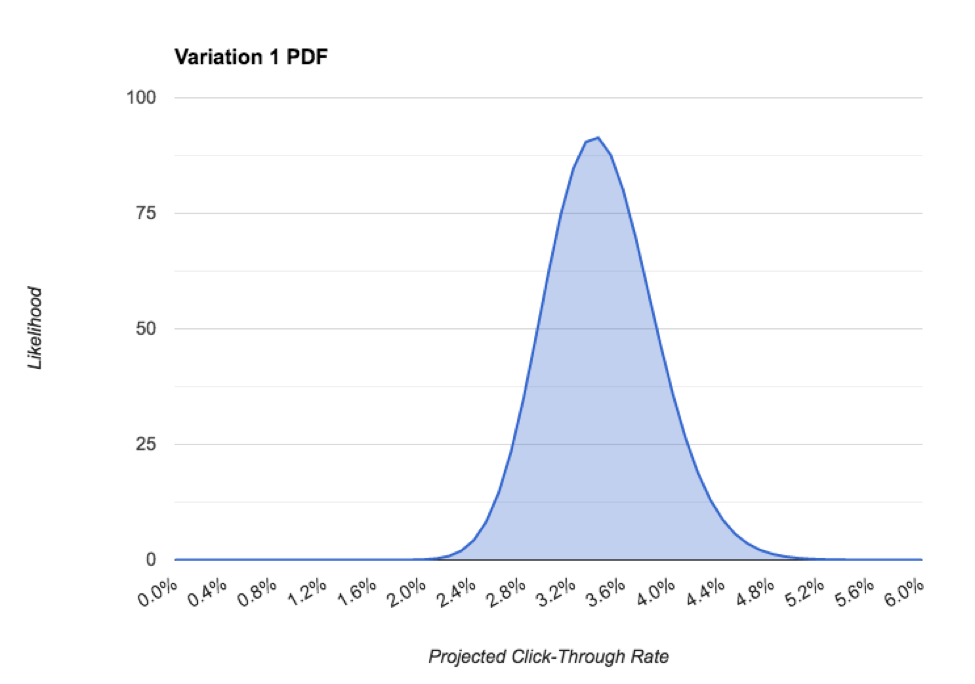
En el PDF anterior, podemos ver la tasa más probable de clic para este post es de aproximadamente 3,4% medir es el intervalo creíble, que es la distribución del 95% del PDF, que en nuestro caso es aproximadamente 2,2%. A medida que recopilamos más datos y nos volvemos más confiados en nuestra predicción, la precisión mejora, lo cual es crítico para realmente escoger a un ganador. Haremos lo siguiente.
Cálculo de la probabilidad
Por fin hemos llegado. Es hora de averiguar si nuestra mejor variación es en realidad un ganador! Empecemos por visualizarlo.
Aquí está el PDF de ambas variaciones, en un gráfico:
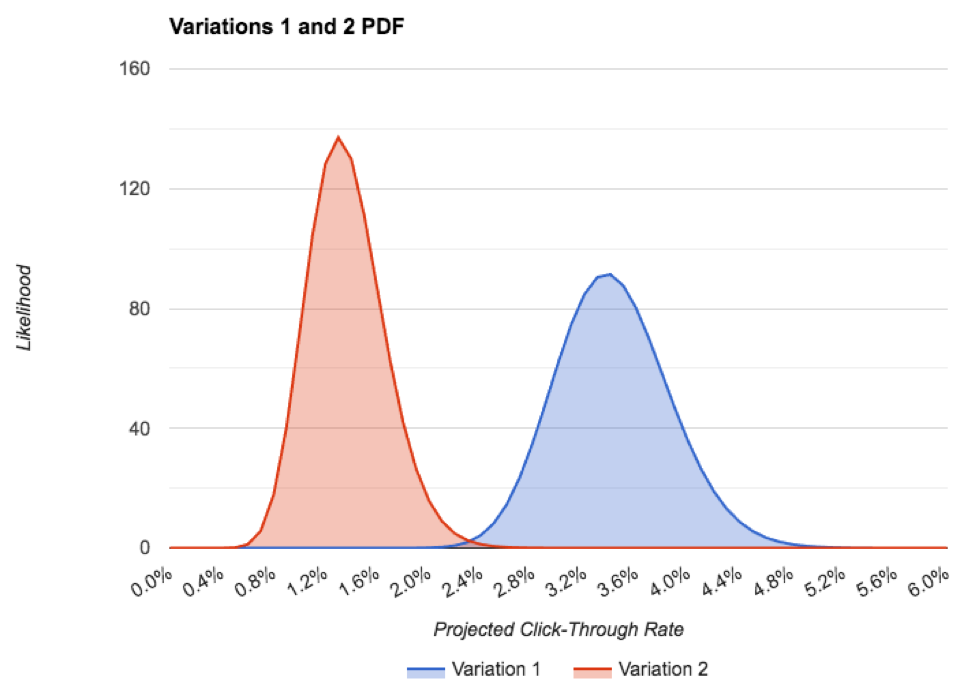
Se puede ver que la precisión de la variación 1 es menor que la variación 2, a pesar de que tenemos un poco más de datos. Esto se debe a que se ha desviado bastante lejos de la tasa esperada, previa de clic. Aún así, no hay casi ninguna coincidencia entre los PDFs, que es una muy buena cosa para nuestra prueba!
La única forma en que la variación 2 es realmente mejor que la variación 1 es si la tasa real de variación 2 en el futuro es superior al 2% y la tasa real de variación de clics 1 en el futuro es inferior a 2,2%, cada una de las cuales es muy improbable. Esto se representa por la pequeña superposición de los dos PDFs. Para que ambas anomalías ocurran sería como voltear docenas de cabezas en una fila en una moneda justa. No va a pasar.
Así que en este punto, estamos muy seguros de que la variación 1 es el ganador y que debe conducir alrededor de un 3,4% CTR, versus variación 2 ' s 1,4%.
Ahora podemos verlo, vamos a calcularlo.
La manera divertida (lenta)
La manera divertida de medir la probabilidad de que una variación es realmente mejor que la otra es ejecutar una simulación de Monte Carlo cadena de Markov. Para nuestros resultados de la prueba, después de 1 millón iteraciones, conseguimos una probabilidad 0,999 que la variación 1 es la mejor. ¡Gran!
El inconveniente es un MCMC realmente requiere software para hacer algo un millón de veces. ¿Quién tiene esa clase de tiempo?
La manera aburrida (rápida)
Afortunadamente para nosotros, hay gente inteligente que ha ideado fórmulas inteligentes así que no tenemos que simular nosotros mismos.
Después de enchufar nuestros números y esperar un par de milisegundos, vemos que la variación 1 es mejor que 2 con una probabilidad de 1,0. ¡ La victoria es nuestra!
Vamos a recapitular todos los pasos que hemos tomado para concluir que nuestra prueba es exitosa:
- Formamos una creencia previa de la tasa esperada de click-through de nuestros posts, representado por los parámetros α y β
- Mostramos cada variación a una muestra representativa de nuestra audiencia, recolectando clic y alcanzando datos de Facebook a medida que íbamos
- Utilizamos nuestra creencia previa y los datos que sacamos de nuestra prueba para calcular cada post es probable clic a través de la tasa
- Miramos el PDF de nuestros traseros para asegurarnos de que tuviéramos suficientes datos, según lo informado por una precisión requerida
- Utilizamos una fórmula de lujo para calcular la probabilidad de que nuestra variación de mejor rendimiento es en realidad la mejor
Ahora es el momento de @channel #general los resultados de su prueba de A/B, sabiendo que su ganador es legítimo y que conducirá más compromiso social y clics de nuevo a su contenido asombroso. Lo que es de esperar de los perros rosas.
Lectura adicional
Los conceptos en esta entrada de blog y los métodos utilizados por nuestra herramienta se beneficiaron enormemente del trabajo reflexivo de varios científicos y estadísticos de datos. Recomendamos encarecidamente profundizar en estos conceptos leyendo su trabajo:
- Cómo funciona la prueba A/B
- Ignorante no más: curso intensivo sobre estadísticas de pruebas A/B
- La significación estadística no equivale a validez
- Cómo no ejecutar una prueba A/B
- Pruebas A/B con modelos jerárquicos en Python
- Bandidos bayesianos
- Asesoramiento estadístico para pruebas A/B
- Fórmulas para la prueba de A/B Bayesiano
- Comprensión del modelado jerárquico Bayesiano empírico
- Esta serie entera, "usando estadísticas del béisbol" es excepcional.
¿quieres saber más?
A/B probar su contenido en Facebook es un tema complejo. Te tenemos cubierto, puedes leer más sobre:
- Optimización de contenido para el algoritmo cambiante de Facebook
- Fabricación efectiva copia de introducción
- Diseñando anuncios de Facebook dignos de click
Póngase en el asiento del conductor y comience A/B probando su contenido para Facebook. Le toma menos de un minuto para inscribirse en nuestro Pruebas A/B para redes sociales Herramienta y es completamente gratis, ¿por qué no dar una vuelta?