É mais fácil de explicar teste social A/B usando esta analogia:
Finge que nunca tinhas visto um cão antes. (Trabalha comigo aqui.) Estás na tua calçada favorita e vê um a passar. E é cor-de-rosa. Baseado em não ter conhecimento prévio de como os cães devem ser, provavelmente agora acreditas que todos os cães são cor-de-rosa. Que esquisito.
Depois vês um segundo cão a passar. É preto. Com este novo conhecimento, você agora considera que 50% dos cães são rosa e 50% são pretos. Você não tem como saber neste momento que um cão cor-de-rosa é um outlier, algo que você pode nunca mais ver novamente.
Vamos trazê-lo de volta à realidade. Tu sabes como são os cães. Quando se vê um cão cor-de-rosa, reconhece-se imediatamente que é invulgar, de facto, impossível sem o corante. No entanto, pode agora permitir que uma pequena percentagem de cães seja cor-de-rosa. Parabéns, você aplicou o pensamento Bayesiano à cor dos cães!
O que isso tem a ver com os testes A/B? Por mais óbvio que seja para nós reconhecer outliers na cor dos cães, é muito mais difícil aplicar este pensamento quando olhamos para conversões, cliques ou engajamento. Vamos tomar um exemplo.
Em vez de ficar na calçada a apanhar ar fresco, está agora sentado à sua secretária, a observar os resultados do seu último teste A/B. Você vê que a variação 1 do seu teste tem uma taxa respeitável de 5% de click-through. A variação 2 parece ainda melhor, com 26%. Você se dá um tapinha nas costas para encontrar a manchete que vai engajar 400% melhor!
"Mas espera", estou a ouvir-te dizer. "Uma taxa de 26% de click-through? Isso parece-se muito com um cão cor-de-rosa." E, na verdade, provavelmente é. Agora você aplicou o pensamento Bayesiano aos testes A/B, e ao fazer isso, você se impediu de enviar aquela mensagem @channel Slack proclamando sua proeza nos testes A/B. Ao invés disso, você aplicará primeiro uma análise rigorosa aos seus resultados.
Aqui está como fazer isso.
Nosso objetivo
Vamos tornar isto um pouco mais concreto. Vamos usar um exemplo real, cortesia de um dos nossos parceiros editoriais. Ferramenta Social A/B para fazer os testes A/B. Este cliente em particular quer testar a cópia de introdução de um post do Facebook. Aqui estão as variações:
Variação 1:
"Siga Mikey Rencz, Mikkel Bang e Mark Sollors no episódio três de Burton Presents. Veja abaixo."
Variação 2:
"A vida de um profissional Burton."
Queremos saber qual destas duas mensagens terá melhor desempenho no Facebook, e por quanto. Para fazer isso, publicaremos cada variação para uma pequena amostra representativa do público da editora e acompanharemos o desempenho de cada variação ao longo do tempo. Felizmente, Social A/B automatiza este processo para si. Após algum tempo (geralmente alguns minutos), receberemos dados do Facebook. É aí que a verdadeira diversão começa.
A abordagem ingénua à análise de resultados de testes A/B
A maneira mais fácil de calcular o desempenho de um posto é a seguinte:
- Obtenha os cliques e alcance para cada variação
- Divida os cliques por alcance para obter a taxa de cliques (CTR)
- Calcule o quanto um é melhor do que o outro
Os testadores mais sofisticados usarão uma calculadora de tamanho de amostra para validar que a amostra é suficientemente grande para ser significativa. Este é um passo crítico. Mas nós não acreditamos que seja suficiente. Eis a razão...
Digamos que depois de expor as duas variações a uma audiência representativa de amostra durante 20 minutos, recebemos estes resultados:
- Variação 1: 46 clicks, 866 impressões = 5,3% CTR
- Variação 2: 8 clicks, 676 impressões = 1,2% CTR
A variação 1 superou a variação 2 neste exemplo em 340%. Legítima? Um teste rápido de chi-quadrado valida que temos dados suficientes para formar uma conclusão, e por isso nos sentimos confiantes.
Mas agora vamos fazer o teste do cão cor-de-rosa. Quando foi a última vez que você teve uma taxa de cliques superior a 5%? Nunca? Ok, este post é uma notícia de última hora, ou sobre o vestido branco e dourado? Não? É uma história sobre cães cor-de-rosa? Talvez a taxa de cliques valha mais uma olhadela.
Esta abordagem ignora a realidade do que geralmente acontece em seus postos, abrindo a porta para suposições extremamente imprecisas. Pode ainda prever com precisão a melhor variação, mas quanto melhor? Se a variação 1 tiver 46 clicks em 866 impressões, ela realmente terá 460 em 8.660 impressões? É possível, mas ao formar uma decisão editorial importante e reivindicar vitórias nos testes A/B, é melhor transmitir um otimismo cauteloso do que uma exuberância esperançosa. Portanto, vamos usar os mesmos dados, mas levemos em conta nosso conhecimento prévio.
A abordagem Bayesiana
Quando reconheceu o cão cor-de-rosa como uma anomalia, fê-lo devido ao seu conhecimento prévio (ou crença) sobre a cor natural dos cães. Você também adicionou este novo ponto de dados (um único cão cor-de-rosa) ao seu conhecimento, fazendo dele a nova crença anterior para o seu "eu" futuro. Este é o conceito fundamental do pensamento Bayesiano. E é o que precisamos fazer ao analisar os resultados dos testes. Por quê? Porque você tem uma tonelada de conhecimento sobre como seu conteúdo e seu público geralmente se comportam. Não há razão para ignorar esse conhecimento ao prever o desempenho futuro.
O primeiro desafio que enfrentamos é quantificar nossa crença anterior sobre o desempenho dos posts no Facebook. Esta crença anterior matemática precisa representar duas coisas:
- A sua taxa de cliques habitual
- A variação típica das taxas de click-through entre as mensagens
Para a editora do nosso exemplo, a maioria dos posts do Facebook vê entre 1% e 2% de taxa de cliques, sem muita variação. Poderíamos representar isso como uma média e um desvio padrão, mas mais úteis para os cálculos que precisamos fazer são representar o conhecimento como o que se chama parâmetros alfa (α) e beta (β). Comece: magia.
O α e o β para esta editora são 12,92 e 842,22, respectivamente. Discutiremos como estes são calculados num dia de chuva. Por enquanto, saiba apenas que eles representam a taxa de cliques esperada de um post, e que sua magnitude está inversamente correlacionada com a variação da taxa de cliques.
Para verificar o nosso trabalho, vamos usar o nosso α e β para calcular a nossa taxa de cliques esperada. Podemos fazer isso com uma fórmula simples:
CTR esperado = α / (α + β) = 12,92 / (12,92 + 842,22) = 1,5%
Isto corresponde à nossa crença anterior sobre a performance da editora. Como podemos usar isto para prever as taxas futuras de cliques em nossos posts? É mágico porque é muito simples:
CTR previsto = (clicks + α) / (reach + α + β)
O quê? Matemática do 8º ano? Tenho de adorar. Então vamos usar isto para calcular a nossa taxa de cliques prevista, pois os dados vieram do nosso teste do mundo real que tocamos acima:
| Ata | Variação 1 Cliques/Reach - CTR | Variação 2 Cliques/Reach - CTR | Variação 1 CTR Previsto | Variação 2 CTR Previsto |
|---|
| 0 | 0/0 – 0% | 0/0 – 0% | 1.5% | 1.5% |
| 5 | 2/200 – 1% | 4/174 – 2.3% | 1.41% | 1.64% |
| 10 | 12/260 – 4.6% | 4/290 – 1.4% | 2.23% | 1.48% |
| 15 | 36/698 – 5.2% | 6/578 – 1% | 3.15% | 1.32% |
| 20 | 46/866 – 5.3% | 8/676 – 1.2% | 3.42% | 1.37% |
No minuto 0, antes de testarmos nosso posto, a fórmula nos dá uma taxa de click-through prevista que é igual à nossa crença anterior. Faz sentido, pois se não tivermos nenhuma informação nova, o nosso resultado mais provável é igual à nossa crença anterior.
Agora dê uma olhada no minuto 20, onde observamos uma taxa de 5,3% de click-through para a variação 1. É tentador proclamar como essa variação é boa, mas quando levamos em conta nosso conhecimento anterior - tanto a taxa média de cliques para essa editora quanto a variação esperada, como representada em nossos parâmetros α e β - vemos que é muito mais provável que a taxa real de cliques seja de 3,4%.
Para completar a intuição sobre este exemplo, vamos fingir que temos uma população muito maior, e que a variação 1 da taxa de click-through é na verdade 5,3%. Para ver como esta fórmula funciona, vamos multiplicar os resultados da variação 1 de 20 minutos por 1.000.
CTR previsto = (46000 + 12,92) / (866.000 + 19,92 + 842,22)
CTR previsto = 5,3%
Você pode notar duas coisas:
- À medida que obtemos mais dados, ficamos mais confiantes de que a taxa de click-through observada é realmente a nossa taxa de click-through prevista.
- Quanto maiores forem os parâmetros α e β, mais dados precisamos para mover a nossa previsão
Parabéns, você completou a parte Bayesiana da análise! Agora vamos usar as nossas previsões para escolher um vencedor.
Medição de precisão
Antes de falarmos de precisão, temos de falar de funções de densidade de probabilidade. Contenha-se, a parte mais emocionante ainda está por vir!
Os parâmetros α e β formam a base para a função de densidade de probabilidade (PDF) de uma distribuição beta. Em inglês, isto diz-nos a probabilidade de que a nossa taxa de click-through seja um determinado valor. Exemplo:
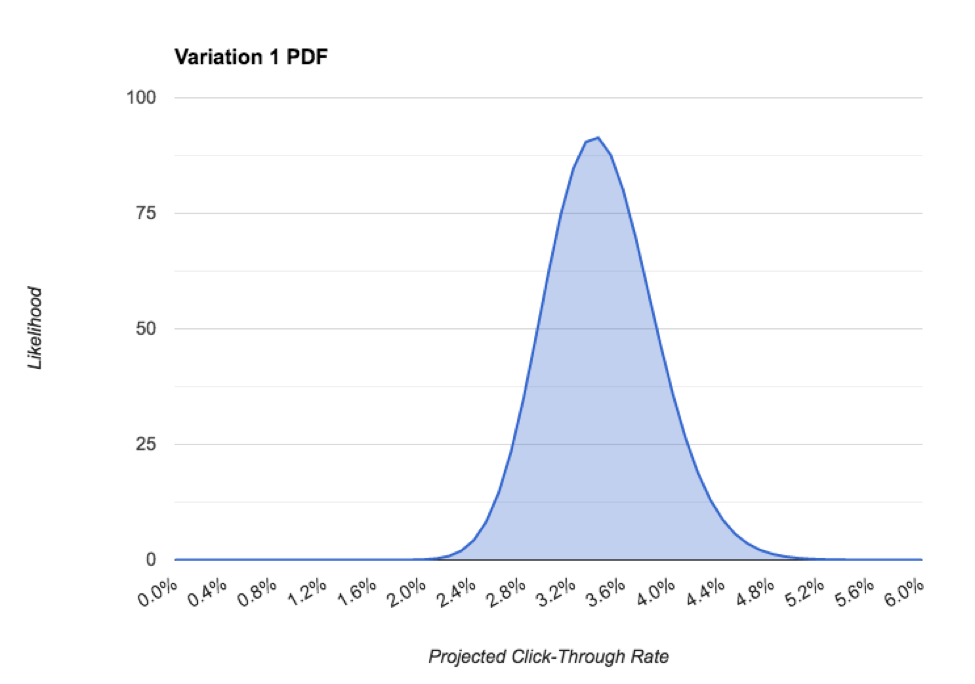
No PDF acima, podemos ver que a taxa de click-through mais provável para este post é de cerca de 3,4%. medir é o intervalo credívelque é a distribuição de 95% do PDF, que no nosso caso é de cerca de 2,2%. À medida que recolhemos mais dados e nos tornamos mais confiantes na nossa previsão, a precisão melhora, o que é fundamental para realmente escolher um vencedor. A seguir, vamos abordar isso.
Cálculo da probabilidade
Finalmente chegámos. Está na hora de descobrir se a nossa melhor variação é realmente uma vencedora! Vamos começar por visualizá-la.
Aqui está o PDF de ambas as variações, em um gráfico:
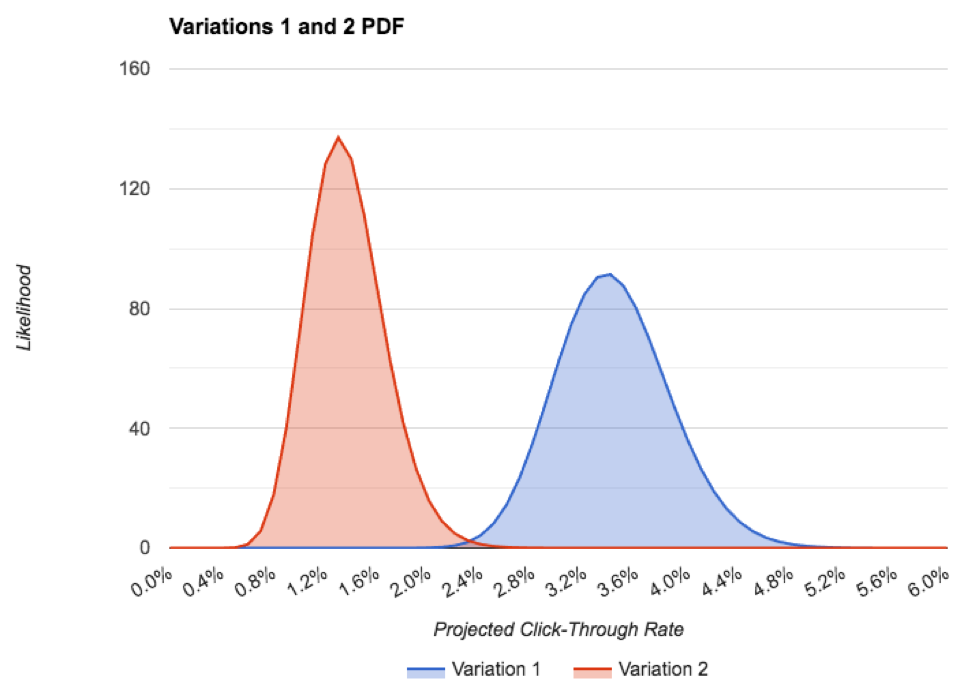
Você pode ver que a precisão da variação 1 é menor que a variação 2, apesar de termos um pouco mais de dados. Isto é porque se afastou bastante da taxa de cliques prévia esperada. Mesmo assim, quase não há sobreposição entre os PDFs, o que é uma coisa muito boa para o nosso teste!
A única maneira da variação 2 ser realmente melhor do que a variação 1 é se a taxa real de cliques futuros da variação 2 foi superior a 2% e a taxa real de cliques futuros da variação 1 foi inferior a cerca de 2,2%, cada uma das quais é altamente improvável. Isto é representado pela pequena sobreposição dos dois PDFs. Para que ambas as anomalias ocorram seria como virar dezenas de cabeças em uma moeda justa. Não vai acontecer.
Portanto, neste momento, estamos muito confiantes de que a variação 1 é a vencedora e que deve conduzir cerca de 3,4% CTR, contra a variação 2 é de 1,4%.
Agora podemos vê-lo, vamos calculá-lo.
A maneira divertida (lenta)
A maneira divertida de medir a probabilidade de uma variação ser realmente melhor do que a outra é executar uma simulação da cadeia de Markov Monte Carlo. Para os nossos resultados de teste, após 1.000.000 iterações, obtemos uma probabilidade de 0,999 de que a variação 1 é a melhor. Ótimo!
O lado negativo é que um MCMC requer software para fazer algo um milhão de vezes. Quem tem esse tipo de tempo?
A maneira chata (rápida)
Felizmente para nós, há pessoas inteligentes que conceberam fórmulas inteligentes para não termos de ser nós a simulá-lo.
Depois de ligar os nossos números e esperar alguns milissegundos, vemos que a variação 1 é melhor que 2 com uma probabilidade de 1.0. A vitória é nossa!
Vamos recapitular todos os passos que demos para concluir que o nosso teste foi bem sucedido:
- Nós formamos uma crença prévia da taxa esperada de click-through dos nossos posts, representada pelos parâmetros α e β
- Mostramos cada variação para uma amostra representativa do nosso público, coletando dados de clique e de alcance do Facebook à medida que íamos
- Usamos nossa crença anterior e os dados que tiramos do nosso teste para calcular a taxa provável de cliques em cada postagem.
- Olhamos para o PDF dos nossos cartazes para nos certificarmos de que tínhamos dados suficientes, conforme informado por uma precisão necessária
- Usamos uma fórmula sofisticada para calcular a probabilidade de que a nossa variação com melhor desempenho é realmente a melhor
Agora é a hora de @channel #general os resultados do seu teste A/B, sabendo que o seu vencedor é legítimo e que ele irá conduzir mais engajamento social e clica de volta para o seu incrível conteúdo. O que esperamos que seja sobre cães cor-de-rosa.
Leitura adicional
Os conceitos neste post de blog e os métodos utilizados pela nossa ferramenta beneficiaram muito com o trabalho cuidadoso de vários cientistas e estatísticos de dados. Recomendamos que mergulhe mais profundamente nestes conceitos, lendo o seu trabalho:
- Como funcionam os testes A/B
- Ignorante Não Mais: Curso de Crash em Estatísticas de Testes A/B
- Significado Estatístico Não Tem Igual Validade
- Como não fazer um teste A/B
- Testes A/B com Modelos Hierárquicos em Python
- Bandidos Bayesianos
- Conselhos Estatísticos para Testes A/B
- Fórmulas para testes Bayesian A/B
- Compreender a modelagem empírica bayesiana hierárquica
- Toda esta série, "usando estatísticas de beisebol" é excelente.
Queres saber mais?
A/B testando seu conteúdo no Facebook é um assunto complexo. Nós te cobrimos - você pode ler mais sobre isso:
- Otimizando o conteúdo para o algoritmo de mudança do Facebook
- Cópia de introdução eficaz
- Projetando anúncios dignos de um clique no Facebook
Coloque-se no lugar do condutor e comece a testar o seu conteúdo para o Facebook. Você leva menos de um minuto para se inscrever para o nosso Ferramenta Social A/B e é completamente grátis - então porque não dar uma volta?