C'est plus facile à expliquer tests sociaux A/B en utilisant cette analogie:
Fais comme si tu n'avais jamais vu de chien. (Travailler avec moi ici.) Vous êtes debout sur votre trottoir préféré et voir un passer. Et c'est rose. Sur la base d'avoir aucune connaissance préalable de ce que les chiens sont censés ressembler, vous probablement maintenant croire que tous les chiens sont roses. C'est bizarre.
Ensuite, vous voyez un deuxième chien passer. Il est noir. Avec cette nouvelle connaissance, vous considérez maintenant que 50% des chiens sont roses et 50% sont noirs. Vous n'avez aucun moyen de savoir à ce stade qu'un chien rose est une aberrante, quelque chose que vous ne reverrez peut-être jamais.
Ramenons-le à la réalité. Tu sais à quoi ressemble un chien. Quand vous voyez un chien rose, vous le reconnaissez immédiatement comme inhabituel, en effet, impossible sans colorant. Cependant, vous pouvez maintenant permettre que certains petit pourcentage de chiens sont roses. Félicitations, vous avez appliqué la pensée bayésienne à la couleur des chiens!
Qu'est-ce que cela a à voir avec les tests A/B? Aussi évident que c'est pour nous de reconnaître les valeurs aberrantes dans la couleur des chiens, il est beaucoup plus difficile d'appliquer cette pensée en regardant les conversions, les clics ou l'engagement. Prenons un exemple.
Au lieu de se tenir sur le trottoir en appréciant l'air frais, vous êtes maintenant assis à votre bureau, en observant les résultats de votre dernier test A/B. Vous voyez que la variation 1 de votre test a un taux de clics respectable de 5%. La variation 2 semble encore meilleure à 26%. Vous vous tape sur le dos pour trouver le titre qui va engager 400% de mieux!
"Mais attendez," je vous entends dire. "Un taux de clics de 26%? C'est sûr ressemble beaucoup à un chien rose. Et en effet il est probablement. Vous avez maintenant appliqué la pensée bayésienne aux tests A/B, et ce faisant, vous vous êtes arrêté d'envoyer ce message @channel Slack proclamant vos prouesses de test A/B. Au lieu de cela, vous allez d'abord appliquer une analyse rigoureuse à vos résultats.
Voici comment le faire.
Notre objectif
Faisons-en un peu plus concrets. Nous allons utiliser un exemple du monde réel courtoisie de l'un de nos partenaires d'édition Outil social A/B pour exécuter des tests A/B. Ce client particulier veut tester la copie d'introduction d'un post Facebook. Voici les variations:
Variante 1:
"Suivez Mikey Rencz, Mikkel Bang, et Mark Sollers autour de l'épisode trois de Burton présente. Regarder ci-dessous.
Variante 2:
"La vie d'un Pro de Burton."
Nous voulons savoir lequel de ces deux postes sera le meilleur rendement sur Facebook, et par combien. Pour ce faire, nous afficherons chaque variation à un petit échantillon représentatif de l'auditoire de l'éditeur et de suivre les performances de chaque variation dans le temps. Heureusement Test A/B pour les réseaux Sociaux automatise ce processus pour vous. Après un certain temps (généralement quelques minutes), nous recevrons des données de Facebook. C'est là que le vrai plaisir commence.
L'approche naïve de l'analyse des résultats des tests A/B
La façon la plus simple de calculer les performances d'un poste est la suivante:
- Obtenez les clics et la portée pour chaque variation
- Diviser les clics par REACH pour obtenir le taux de clic (CTR)
- Calculer combien mieux on est que l'autre
Des testeurs plus sophistiqués utiliseront un calculateur de taille d'échantillon pour valider que l'échantillon est suffisamment grand pour être significatif. C'est une étape cruciale. Mais nous ne croyons pas que c'est suffisant. Voici pourquoi...
Disons que, après avoir exposé les deux variations à un auditoire représentatif de l'échantillon pendant 20 minutes, nous recevons ces résultats:
- Variation 1:46 clics, 866 impressions = 5,3% CTR
- Variation 2:8 clics, 676 impressions = 1,2% CTR
La variation 1 a surperformé la variation 2 dans cet exemple de 340%. Légitime? UN test rapide de Chi-carré valide que nous avons assez de données pour former une conclusion, et ainsi nous sommes confiants.
Mais maintenant, nous allons lui donner le test de chien rose. Quand est la dernière fois que vous avez eu un lecteur de poste de plus de 5% taux de clics? Jamais? OK, est-ce post nouvelles de rupture, ou sur la robe blanche et dorée? Pas? C'est une histoire de chiens roses? Peut-être le clic-through taux vaut un autre regard.
Cette approche ignore la réalité de ce qui se passe habituellement sur vos postes, ouvrant la porte à des hypothèses inexactes. Il peut encore prédire avec précision la meilleure variation, mais comment beaucoup mieux? Si la variation 1 a obtenu 46 clics sur 866 impressions, est-il vraiment obtenir 460 sur 8 660 impressions? C'est possible, mais en formant une décision éditoriale importante et en revendiquant des victoires de test A/B, il est préférable d'air sur le côté de l'optimisme prudent que sur l'exubérance d'espoir. Donc, nous allons utiliser les mêmes données, mais prendre notre connaissance préalable en compte.
L'approche bayésienne
Lorsque vous avez reconnu le chien rose comme une anomalie, vous l'avez fait en raison de votre connaissance préalable (ou de croyance) sur la couleur naturelle des chiens. Vous avez également ajouté ce nouveau point de données (un seul chien rose) à votre connaissance, ce qui en fait la nouvelle croyance avant de votre auto avenir. C'est le concept fondamental de la pensée bayésienne. Et c'est ce que nous devons faire pour analyser les résultats des tests. Pourquoi? Parce que vous avez une tonne de connaissances sur la façon dont votre contenu et le public effectuent habituellement. Il n'y a aucune raison d'ignorer cette connaissance lors de la prévision des performances futures.
Le premier défi auquel nous sommes confrontés est de quantifier notre croyance antérieure sur Facebook post performance. Cette croyance mathématique avant doit représenter deux choses:
- Votre taux de clics habituel
- La variance typique des taux de clics entre les postes
Pour l'éditeur dans notre exemple, la plupart des messages Facebook voir entre 1% et 2% taux de clics, sans beaucoup de variance. Nous pourrions représenter cela comme une moyenne et un écart-type, mais plus utile pour les calculs que nous devons faire sont de représenter les connaissances que ce qu'on appelle alpha (α) et bêta (β) paramètres. BEGIN: Magic.
Les α et β pour cet éditeur sont respectivement 12,92 et 842,22. Nous allons discuter de la façon dont ils sont calculés par un jour pluvieux. Pour l'instant, il suffit de savoir qu'ils représentent le clic attendu à travers le taux d'un poste, et que leur magnitude est inversement corrélée à la variance des taux de clics.
Pour vérifier notre travail, nous allons utiliser notre α et β pour calculer notre taux de clics attendu. Nous pouvons le faire avec une formule simple:
CTR attendu = α/(α + β) = 12,92/(12,92 + 842,22) = 1,5%
Cela correspond à notre croyance antérieure sur la performance post de l'éditeur. Comment pouvons-nous l'utiliser pour prédire les taux de clics futurs sur nos postes? C'est magique parce qu'il est mort simple:
CTR prédit = (clics + α)/(REACH + α + β)
Quel? les maths de 8e? Je dois l'adorer. Donc, nous allons utiliser ce pour calculer notre taux de clics prédit que les données sont venues de notre test du monde réel, nous avons abordé ci-dessus:
| Minute | Variante 1 Clicks/Reach - CTR | Variante 2 Clicks/Reach - CTR | Variante 1 CTR prédit | Variante 2 CTR prédit |
|---|
| 0 | 0/0 – 0% | 0/0 – 0% | 1.5% | 1.5% |
| 5 | 2/200 – 1% | 4/174 – 2.3% | 1.41% | 1.64% |
| 10 | 12/260 – 4.6% | 4/290 – 1.4% | 2.23% | 1.48% |
| 15 | 36/698 – 5.2% | 6/578 – 1% | 3.15% | 1.32% |
| 20 | 46/866 – 5.3% | 8/676 – 1.2% | 3.42% | 1.37% |
A la minute 0, avant que nous ayons testé notre post, la formule nous donne un taux de clics prédit qui est égal à notre croyance antérieure. Logique, puisque si nous n'avons pas de nouvelles informations, notre résultat le plus probable est égal à notre croyance antérieure.
Maintenant, jetez un oeil à la minute 20, où nous avons observé un taux de clics de 5,3% pour la variation 1. Il est tentant de proclamer à quel point cette variation est bonne, mais lorsque nous prenons en compte nos connaissances antérieures, à la fois le taux de clics moyen pour cet éditeur et la variance attendue représentée dans nos paramètres α et β, nous voyons qu'il est beaucoup plus probable que le le taux de clics réel est de 3,4%.
Pour arrondir l'intuition sur cet exemple, imaginons que nous ayons une population beaucoup plus importante, et que le taux de clics de variation 1 soit en fait de 5,3%. Pour voir comment cette formule fonctionne, nous multiplions les résultats de 20 minutes de la variation 1 par 1 000.
CTR prédit = (46000 + 12,92)/(866 000 + 19,92 + 842,22)
CTR prévu = 5,3%
Vous remarquerez peut-être deux choses:
- Comme nous obtenons plus de données, nous devenons plus confiants que le taux de clics observé est en fait notre taux de clics prédit
- Plus les paramètres α et β sont grands, plus nous avons besoin de données pour déplacer notre prédiction
Félicitations, vous avez terminé la partie bayésienne de l'analyse! Maintenant, nous allons utiliser nos prédictions pour choisir un gagnant.
Mesure de la précision
Avant de parler de précision, nous devons parler des fonctions de densité de probabilité. ConTenez-vous, la partie la plus excitante est encore à venir!
Les paramètres α et β forment la base de la fonction de densité de probabilité (PDF) d'une distribution bêta. En anglais, cela nous indique la probabilité que notre taux de clics soit une certaine valeur. Exemple:
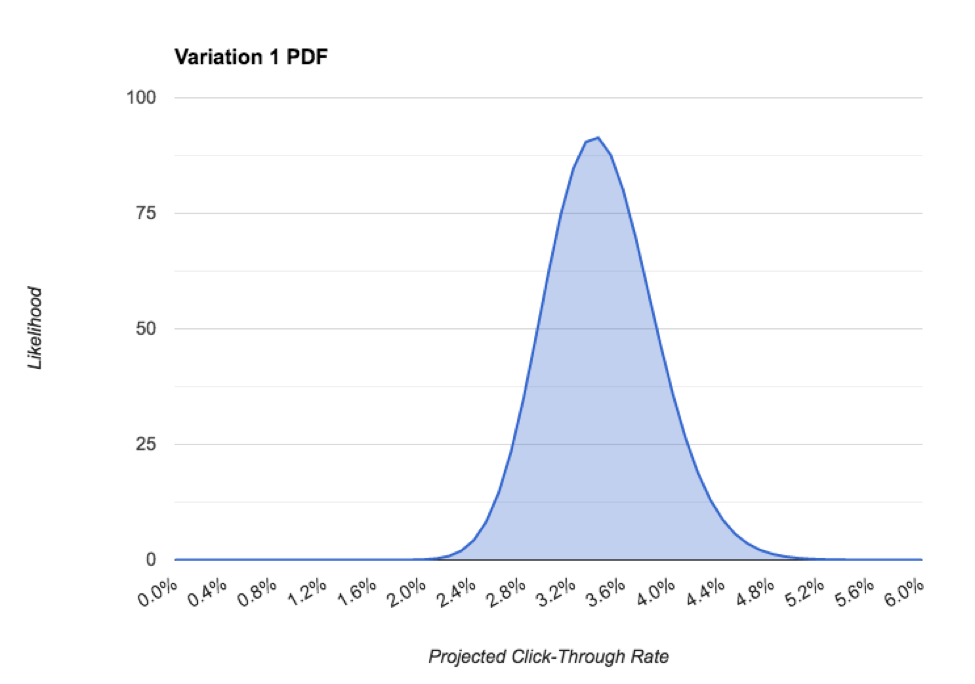
Dans le PDF ci-dessus, nous pouvons voir le taux de clics le plus probable pour ce poste est d'environ 3,4% la mesure est l'intervalle crédible, qui est la distribution de 95% du PDF, qui dans notre cas est d'environ 2,2%. Comme nous recueillons plus de données et de devenir plus confiants dans notre prédiction, la précision s'améliore, ce qui est essentiel pour effectivement choisir un gagnant. On s'attaquera à ça ensuite.
Calcul de la probabilité
Nous sommes enfin arrivés. Il est temps de savoir si notre meilleure variation est en fait un gagnant! Commençons par le visualiser.
Voici le PDF des deux variations, sur un graphique:
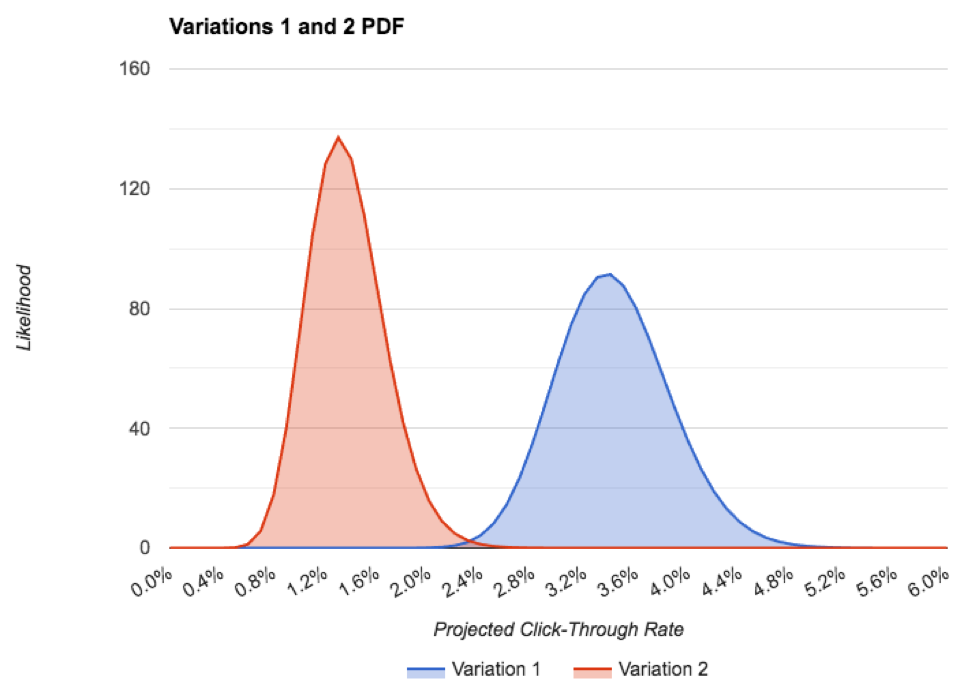
Vous pouvez voir que la précision de la variation 1 est inférieure à la variation 2, même si nous avons un peu plus de données. C'est parce qu'il s'est égaré assez loin de l'attendu, avant le taux de clics. Même encore, il n'y a guère de chevauchement entre les fichiers PDF, ce qui est une très bonne chose pour notre test!
La seule façon dont la variation 2 est en fait meilleure que la variation 1 est si le taux de clics réel à l'avenir de la variation 2 était supérieur à 2% et que le taux de clics à l'avenir réel de la variation 1 était inférieur à environ 2,2%, dont chacun est hautement improbable. Ceci est représenté par le petit chevauchement des deux fichiers PDF. Pour les deux anomalies se produire serait comme renversant des douzaines de têtes dans une rangée sur une pièce de monnaie juste. Ça n'arrivera pas.
Donc, à ce stade, nous sommes très confiants que la variation 1 est le gagnant et qu'il devrait conduire environ un CTR 3,4%, contre la variation 2 de 1,4%.
Maintenant, nous pouvons le voir, nous allons le calculer.
La façon amusante (lente)
La façon amusante de mesurer la probabilité qu'une variation soit vraiment meilleure que l'autre est d'exécuter une simulation de la chaîne de Markov Monte Carlo. Pour nos résultats de test, après 1 million itérations, nous obtenons une probabilité 0,999 que la variation 1 est la meilleure. Grand!
L'inconvénient est un MCMC réellement besoin de logiciels pour faire quelque chose d'un million de fois. Qui a ce genre de temps?
La manière ennuyeuse (rapide)
Heureusement pour nous, il y a des gens intelligents qui ont conçu des formules astucieuses donc, nous n'avons pas à le simuler nous-mêmes.
Après avoir branché nos numéros et attendre quelques millisecondes, nous voyons que la variation 1 est meilleure que 2 avec une probabilité de 1,0. La victoire est à nous!
Nous allons récapituler toutes les étapes que nous avons prises pour conclure notre test est réussie:
- Nous avons formé une croyance antérieure du taux de clics attendu de nos postes, représenté par les paramètres α et β
- Nous avons montré chaque variation à un échantillon représentatif de notre public, la collecte des données Click et REACH de Facebook que nous sommes allés
- Nous avons utilisé notre croyance antérieure et les données que nous avons tirées de notre test pour calculer le taux de clics probable de chaque poste
- Nous avons regardé le PDF de nos postérieurs pour nous assurer que nous disposions de suffisamment de données, telles qu'elles ont été informées par une précision requise
- Nous avons utilisé une formule de fantaisie pour calculer la probabilité que notre variation plus performante soit en fait la meilleure
Il est maintenant temps de @channel #general les résultats de votre test A/B, sachant que votre gagnant est légitime et qu'il va conduire plus d'engagement social et clique sur retour à votre contenu étonnant. Ce qui est, espérons-le, des chiens roses.
Autres lectures
Les concepts de ce billet de blog et les méthodes utilisées par notre outil ont grandement bénéficié du travail réfléchi de plusieurs scientifiques et statisticiens de données. Nous recommandons fortement plonger plus profondément dans ces concepts en lisant leur travail:
- Fonctionnement des tests A/B
- Ignorant pas plus: cours intensif sur les statistiques de tests A/B
- La signification statistique n'est pas égale à la validité
- Comment ne pas exécuter un test A/B
- Test A/B avec des modèles hiérarchiques en Python
- Bandits bayésiens
- Conseils statistiques pour les tests A/B
- Formules pour les tests A/B bayésiens
- Comprendre la modélisation hiérarchique bayésienne empirique
- Cette série entière, "using baseball Statistics" est remarquable.
Vous voulez en savoir plus?
A/B tester votre contenu sur Facebook est un sujet complexe. Nous vous avons couvert-vous pouvez en savoir plus sur:
- Optimisation du contenu pour l'algorithme de change de Facebook
- Rédiger une copie d'intro efficace
- Concevoir des annonces Facebook dignes de clics
Mettez-vous dans le siège du conducteur et démarrez A/B test de votre contenu pour Facebook. Il vous faut moins d'une minute pour vous inscrire à notre Outil social A/B et c'est complètement gratuit, alors pourquoi ne pas faire un tour?