È più facile da spiegare Test Social A/B usando questa analogia:
Fai finta di non aver mai visto un cane. (Lavora con me qui.) Sei in piedi sul tuo marciapiede preferito e ne vedi passare uno. Ed è rosa. Basandosi sul fatto di non avere alcuna conoscenza preliminare di come dovrebbero essere i cani, probabilmente ora credete che tutti i cani siano rosa. Che strano.
Poi si vede passare un secondo cane. È nero. Con questa nuova conoscenza, ora si considera che il 50% dei cani è rosa e il 50% è nero. A questo punto non avete modo di sapere che un cane rosa è un outlier, qualcosa che potreste non vedere mai più.
Riportiamolo alla realtà. Sapete come sono fatti i cani. Quando vedi un cane rosa, lo riconosci subito come insolito, anzi, impossibile senza tintura. Tuttavia, si può ora consentire che una piccola percentuale di cani sono rosa. Congratulazioni, avete applicato il pensiero bayesiano al colore dei cani!
Che cosa ha a che fare questo con i test A/B? Per quanto sia ovvio per noi riconoscere gli outlier nel colore dei cani, è molto più difficile applicare questo pensiero quando si guarda alle conversioni, ai click o all'impegno. Facciamo un esempio.
Invece di stare in piedi sul marciapiede a godersi l'aria fresca, ora siete seduti alla vostra scrivania, osservando i risultati del vostro ultimo test A/B. Vedete che la variazione 1 del vostro test ha un rispettabile tasso di click del 5%. La variazione 2 sembra ancora migliore al 26%. Ti dai una pacca sulla spalla per aver trovato il titolo che si impegna il 400% meglio!
"Ma aspetta", ti sento dire. "Un tasso di click-through del 26%? Di sicuro assomiglia molto a un cane rosa". E probabilmente lo è. Ora avete applicato il pensiero bayesiano ai test A/B, e così facendo vi siete fermati dall'inviare quel messaggio @channel Slack che proclamava la vostra bravura nei test A/B. Invece, per prima cosa, applicherete un'analisi rigorosa ai vostri risultati.
Ecco come fare.
Il nostro obiettivo
Rendiamo la cosa un po' più concreta. Useremo un esempio reale per gentile concessione di uno dei nostri partner editoriali Strumento sociale A/B per eseguire i test A/B. Questo particolare cliente vuole testare la copia di introduzione di un post su Facebook. Ecco le variazioni:
Variazione 1:
"Seguite Mikey Rencz, Mikkel Bang e Mark Sollors nel terzo episodio di Burton Presents. Guarda qui sotto".
Variazione 2:
"La vita di un professionista Burton".
Vogliamo sapere quale di questi due post avrà le migliori prestazioni su Facebook e di quanto. Per fare questo, pubblicheremo ogni variazione su un piccolo campione rappresentativo del pubblico dell'editore e tracceremo le performance di ogni variazione nel tempo. Fortunatamente, Test Social A/B automatizza questo processo per voi. Dopo un po' di tempo (di solito qualche minuto), riceveremo i dati da Facebook. È allora che inizia il vero divertimento.
L'approccio ingenuo all'analisi dei risultati dei test A/B
Il modo più semplice per calcolare le prestazioni di un post è il seguente:
- Ottenere i clic e la portata per ogni variante
- Dividere i clic per portata per ottenere il click-through rate (CTR)
- Calcolare quanto è migliore l'uno rispetto all'altro
I tester più sofisticati utilizzeranno un calcolatore di dimensioni del campione per convalidare che il campione è abbastanza grande da essere significativo. Questo è un passo fondamentale. Ma non crediamo che sia sufficiente. Ecco perché...
Diciamo che dopo aver esposto le due varianti a un pubblico campione rappresentativo per 20 minuti, riceviamo questi risultati:
- Variazione 1: 46 click, 866 impressioni = 5,3% CTR
- Variazione 2: 8 click, 676 impressioni = 1,2% CTR
La variazione 1 ha superato la variazione 2 in questo esempio del 340%. Legittima? Un rapido test chi-squared convalida che abbiamo abbastanza dati per formulare una conclusione, e quindi ci sentiamo sicuri.
Ma ora facciamo il test del cane rosa. Quand'è stata l'ultima volta che hai avuto un post drive con un tasso di click superiore al 5%? Mai? Ok, questo post è una notizia dell'ultima ora, o su l'abito bianco e oro? No? È una storia di cani rosa? Forse il click-through rate vale un altro sguardo.
Questo approccio ignora la realtà di ciò che accade di solito sui vostri posti di lavoro, aprendo la porta a supposizioni del tutto imprecise. Può ancora prevedere con precisione la migliore variazione, ma quanto migliore? Se la variazione 1 ha ottenuto 46 clic su 866 impressioni, ne otterrà davvero 460 su 8.660? È possibile, ma quando si prende una decisione editoriale importante e si rivendicano vittorie di test A/B, è meglio andare in onda sul versante del cauto ottimismo che su quello dell'esuberanza speranzosa. Quindi usiamo gli stessi dati, ma teniamo conto delle nostre conoscenze precedenti.
L'approccio bayesiano
Quando avete riconosciuto il cane rosa come un'anomalia, lo avete fatto a causa della vostra precedente conoscenza (o convinzione) del colore naturale dei cani. Avete anche aggiunto questo nuovo punto di dati (un singolo cane rosa) alla vostra conoscenza, rendendolo la nuova credenza precedente per il vostro futuro. Questo è il concetto fondamentale del pensiero bayesiano. Ed è ciò che dobbiamo fare quando analizziamo i risultati dei test. Perché? Perché avete una tonnellata di conoscenze su come i vostri contenuti e il vostro pubblico di solito si comportano. Non c'è motivo di ignorare questa conoscenza quando si prevede il rendimento futuro.
La prima sfida che dobbiamo affrontare è quella di quantificare le nostre convinzioni precedenti sulla performance dei post di Facebook. Questa convinzione matematica precedente deve rappresentare due cose:
- Il tuo solito tasso di clic
- La tipica varianza dei tassi di click-through tra i messaggi
Per l'editore nel nostro esempio, la maggior parte dei post di Facebook vede una percentuale di clic tra l'1% e il 2%, senza molte variazioni. Potremmo rappresentare questo come una media e una deviazione standard, ma più utile per i calcoli che dobbiamo fare è rappresentare la conoscenza come i cosiddetti parametri alfa (α) e beta (β). Cominciamo con la magia.
Gli α e i β per questo editore sono rispettivamente 12,92 e 842,22. Discuteremo come questi sono calcolati in un giorno di pioggia. Per ora, sappiate che rappresentano il tasso di click-through rate atteso di un post, e che la loro grandezza è inversamente correlata alla varianza dei tassi di click-through rate.
Per verificare il nostro lavoro, usiamo i nostri α e β per calcolare il nostro tasso di click-through previsto. Possiamo farlo con una semplice formula:
CTR previsto = α / (α + β) = 12,92 / (12,92 + 842,22) = 1,5%.
Questo coincide con la nostra precedente convinzione sulla performance dell'editore dopo la pubblicazione. Come possiamo usarlo per prevedere le future percentuali di clic sui nostri post? È una magia perché è molto semplice:
CTR previsto = (clic + α) / (portata + α + β)
Cosa? Matematica di terza media? Da non crederci. Quindi usiamo questo per calcolare il nostro tasso di click previsto, dato che i dati sono arrivati dal nostro test del mondo reale che abbiamo toccato sopra:
| Minuto | Variazione 1 Clicchi/Raggiungi - CTR | Variazione 2 Clicchi/Raggiungi - CTR | Variazione 1 CTR previsto | Variazione 2 CTR previsto |
|---|
| 0 | 0/0 – 0% | 0/0 – 0% | 1.5% | 1.5% |
| 5 | 2/200 – 1% | 4/174 – 2.3% | 1.41% | 1.64% |
| 10 | 12/260 – 4.6% | 4/290 – 1.4% | 2.23% | 1.48% |
| 15 | 36/698 – 5.2% | 6/578 – 1% | 3.15% | 1.32% |
| 20 | 46/866 – 5.3% | 8/676 – 1.2% | 3.42% | 1.37% |
Al minuto 0, prima di aver testato il nostro post, la formula ci dà un tasso di click previsto che è pari alla nostra convinzione precedente. Ha senso, perché se non abbiamo nuove informazioni, il nostro risultato più probabile è uguale alla nostra convinzione precedente.
Ora date un'occhiata al minuto 20, dove abbiamo osservato un tasso di click del 5,3% per la variazione 1. Si è tentati di proclamare quanto sia buona questa variazione, ma quando prendiamo in considerazione le nostre conoscenze precedenti - sia il tasso medio di click-through rate per questo editore, sia la varianza attesa come rappresentata nei nostri parametri α e β - vediamo che è molto più probabile che l'effettivo tasso di click-through rate sia del 3,4%.
Per completare l'intuizione su questo esempio, facciamo finta di avere una popolazione molto più numerosa, e che il tasso di click della variazione 1 sia in realtà del 5,3%. Per vedere come funziona questa formula, moltiplicheremo i risultati della variazione 1 di 20 minuti per 1.000.
CTR previsto = (46000 + 12,92) / (866.000 + 19,92 + 842,22)
CTR previsto = 5,3 %.
Si possono notare due cose:
- Man mano che otteniamo più dati, diventiamo più sicuri che il click-through rate osservato sia effettivamente il nostro tasso di click-through rate previsto
- Più grandi sono i parametri α e β, più dati abbiamo bisogno di spostare la nostra previsione
Congratulazioni, avete completato la parte bayesiana dell'analisi! Ora usiamo le nostre previsioni per scegliere un vincitore.
Precisione di misura
Prima di parlare di precisione, dobbiamo parlare delle funzioni di densità di probabilità. Contenetevi, la parte più eccitante deve ancora venire!
I parametri α e β costituiscono la base per la funzione di densità di probabilità (PDF) di una distribuzione beta. In inglese, questo ci dice la probabilità che il nostro tasso di click sia un certo valore. Esempio:
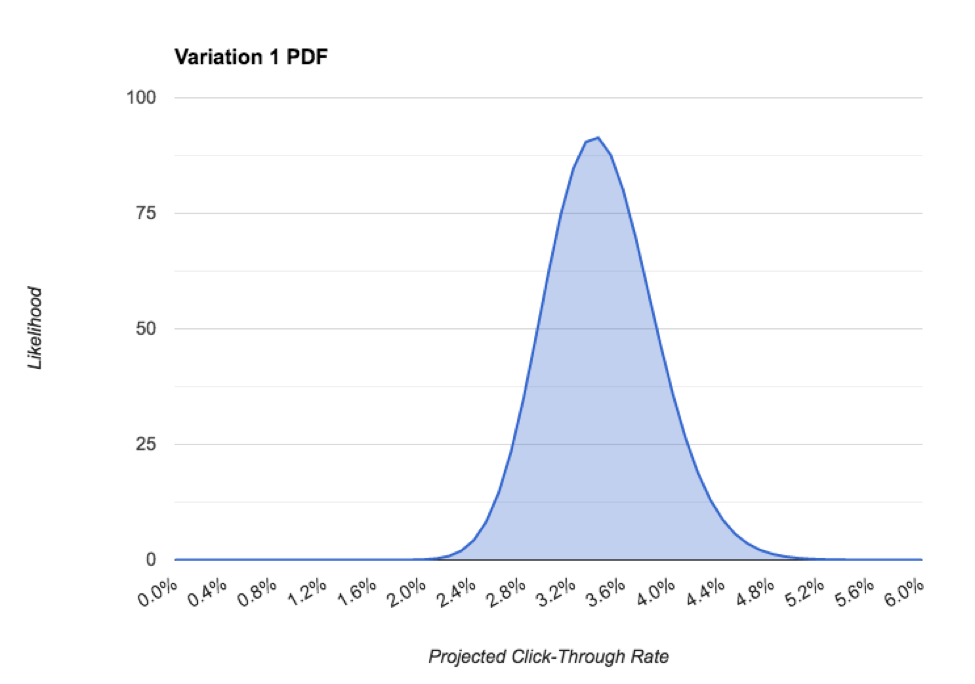
Nel PDF sopra riportato, possiamo vedere che il tasso di clic più probabile per questo post è di circa il 3,4%. la misurazione è l'intervallo credibileche è la distribuzione del 95% del PDF, che nel nostro caso è circa il 2,2%. Man mano che raccogliamo più dati e diventiamo più sicuri della nostra previsione, la precisione migliora, il che è fondamentale per scegliere effettivamente un vincitore. Affronteremo anche questo aspetto.
Calcolo della probabilità
Siamo finalmente arrivati. È ora di capire se la nostra variante migliore è davvero vincente! Cominciamo a visualizzarla.
Ecco il PDF di entrambe le varianti, in un unico grafico:
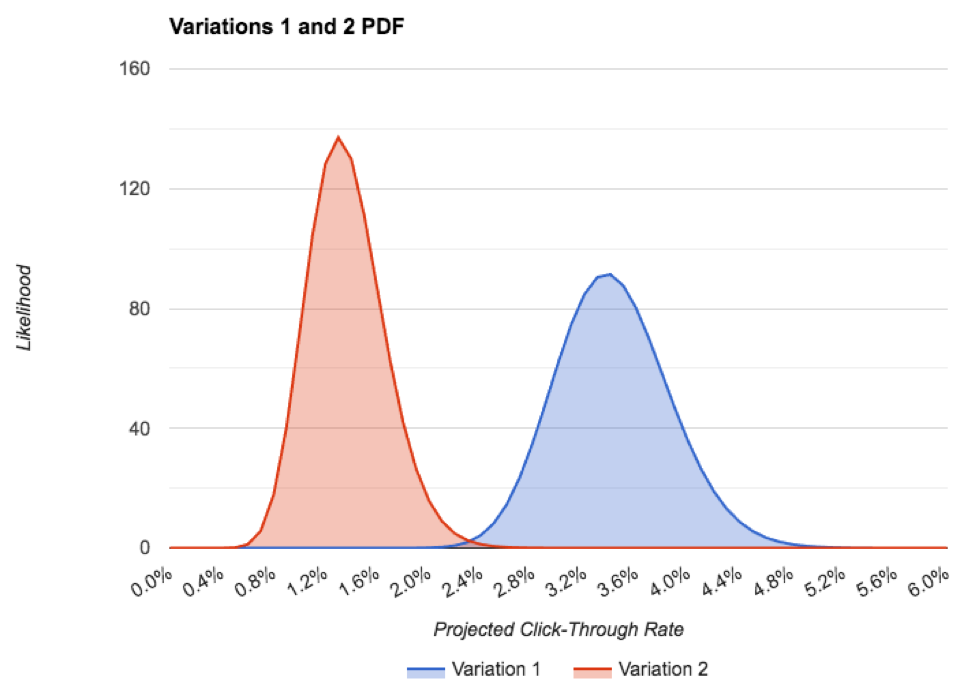
Si può notare che la precisione della variazione 1 è inferiore alla variazione 2, anche se abbiamo un po' più di dati. Ciò è dovuto al fatto che si è allontanata molto dal tasso di click-through previsto in precedenza. Anche in questo caso, non c'è quasi nessuna sovrapposizione tra i PDF, il che è un'ottima cosa per il nostro test!
L'unico modo in cui la variazione 2 è in realtà migliore della variazione 1 è se l'effettivo tasso futuro di click-through della variazione 2 è superiore al 2% e l'effettivo tasso futuro di click-through della variazione 1 è inferiore a circa il 2,2%, ognuno dei quali è altamente improbabile. Ciò è rappresentato dalla piccola sovrapposizione dei due PDF. Per entrambe le anomalie sarebbe come capovolgere dozzine di teste in fila su una moneta equa. Non accadrà.
Quindi, a questo punto, siamo molto fiduciosi che la variazione 1 sia la vincitrice e che dovrebbe portare circa un CTR del 3,4%, contro l'1,4% della variazione 2.
Ora lo vediamo, calcoliamolo.
Il modo divertente (lento)
Il modo divertente per misurare la probabilità che una variazione sia davvero migliore dell'altra è eseguire una simulazione di Markov Chain Monte Carlo. Per i risultati dei nostri test, dopo 1.000.000 di iterazioni, otteniamo una probabilità di 0,999 che la variazione 1 sia la migliore. Fantastico!
Il lato negativo è che un MCMC richiede in realtà un software per fare qualcosa un milione di volte. Chi ha tutto questo tempo?
Il modo noioso (veloce)
Per nostra fortuna, ci sono persone intelligenti che hanno ideato formule intelligenti in modo da non doverlo simulare noi stessi.
Dopo aver collegato i nostri numeri e aver aspettato un paio di millisecondi, vediamo che la variazione 1 è migliore di 2 con una probabilità di 1.0. La vittoria è nostra!
Ricapitoliamo tutti i passi che abbiamo fatto per concludere con successo il nostro test:
- Abbiamo formato una precedente convinzione del tasso di click-through previsto per i nostri post, rappresentato dai parametri α e β
- Abbiamo mostrato ogni variazione a un campione rappresentativo del nostro pubblico, raccogliendo i dati di click e reach da Facebook mentre andavamo
- Abbiamo usato la nostra convinzione precedente e i dati che abbiamo estratto dal nostro test per calcolare il probabile tasso di click through di ogni post
- Abbiamo guardato il PDF dei nostri posteri per assicurarci di avere dati sufficienti, informati con la precisione richiesta
- Abbiamo usato una formula di fantasia per calcolare la probabilità che la nostra variazione con migliori prestazioni sia effettivamente la migliore
Ora è il momento di @channel #general i risultati del vostro test A/B, sapendo che il vostro vincitore è legittimo e che porterà più impegno sociale e cliccherà di nuovo sui vostri incredibili contenuti. Che si spera riguardi i cani rosa.
Ulteriori letture
I concetti contenuti in questo post del blog e i metodi utilizzati dal nostro strumento hanno tratto grande beneficio dal ponderato lavoro di diversi scienziati dei dati e statistici. Raccomandiamo vivamente di approfondire questi concetti leggendo il loro lavoro:
- Come funzionano i test A/B
- Ignorante No More: Corso Crash sulle statistiche dei test A/B
- Il significato statistico non è uguale alla validità
- Come non eseguire un test A/B
- Test A/B con modelli gerarchici in Python
- Banditi Bayesiani
- Consigli statistici per i test A/B
- Formule per il test A/B Bayesiano
- Comprensione della modellazione gerarchica empirica bayesiana
- L'intera serie, "utilizzando le statistiche del baseball" è eccezionale.
Volete saperne di più?
A/B testare i tuoi contenuti su Facebook è un argomento complesso. Ti copriamo noi - puoi saperne di più:
- Ottimizzazione dei contenuti per l'algoritmo di modifica di Facebook
- Creazione di una copia introduttiva efficace
- Progettare annunci pubblicitari su Facebook degni di essere cliccati
Mettiti al posto di guida e inizia A/B testando i tuoi contenuti per Facebook. Ti ci vuole meno di un minuto per iscriverti al nostro Strumento Social A/B ed è completamente gratuito, quindi perché non fare un giro?